The first post in this series is here. The previous post in this series is here. The next post in this series is here.
In this series, we explain scientific foundations of neural networks technologies to dive into their use of natural language processing and neural machine translation.
Part Nine explained why the vector space structure of word vectors is something quite useful for machine translation. Today we’ll continue with that notion explaining the M function introduced last time.
M Function and Trans Function
Function ‘M‘ maps word vectors from one language (in our case English) to their respective translated word vectors in a different language (Spanish). Hence, M acts as a dictionary, with the extra ingredient of being linear, which means
M(x+y) = M(x) + M(y)
Please recall the function trans, which does the same thing, only with the words themselves, rather than their vector representations. This can be neatly expressed by the following formula
trans = vec-1 M vec
Next, I pointed out three problems one encounters with ordinary dictionaries, namely
- New words pop into existence every day, and it is difficult to keep track of them.
- If you have multiple candidates, it is not clear how to choose the best one.
- There might be mistakes, which go unnoticed, especially if the word is rare.
I promised that M can help us with these, so let’s start with the first bullet point. The appearance of ‘out-of-dictionary words’, i.e. words that are not in the dictionary. This happens when new words enter the language. The example from last time illustrates nicely how to solve this problem. We had the relation
vec(‘queen’) = vec(‘king’) – vec(‘man’) + vec(woman’)
and we could deduce from
M(vec(‘queen’)) = vec(‘rey’) – vec(‘hombre’) + vec(‘mujer’)
Hence, only by knowing the correct translation of ‘king’, ‘man’ and ‘woman’, we could translate ‘queen’ (the translation being ‘reina’), with linearity being the key. So, if a new word appears in both languages (in the above example ‘queen’/’reina’), we might still be able to translate it, as long as we can express it as ‘linear combination’ of old words.
But remember, our vectors spaces are full of syntactic and semantic relation, and so this seems to be a very promising idea indeed. Admittedly, for this to work, the vectors of the new words must be known. However, as we have seen in previous blogs, learning word representations is something rather automatic and does not require human intervention.
You might have noticed that I cheated a bit (again!). Recall, that when you add two-word vectors you basically never get another word vector. You must look for the closest neighbour, to get a meaningful result. Similarly, if you take a word vector of the source language and apply M, you will never get another word vector in the target language. You must again look for the closest neighbour.
Luckily, this fact can be used to solve yet another problem of ordinary dictionaries. You can think of the distance to the closest word vector in the target language as a measure of the accuracy of the translation. If the distance is very small, the translation is probably spot on. If it is bigger than usual, then it might be inaccurate.
Let’s say you can also consider the ten-word vectors that are closest to that what M gives you. This provides you with a ranking of possible translations together with a number (the distance) telling you how trustworthy the result is. This idea can be refined to get a measure of the accuracy of the translation of not just one word or phrase, but a whole text.
M Stands For Matrix
Finally, this leads us to the last bullet point. How to find mistakes in a dictionary? Well, look it up. But that is obviously circular. You might check other sources but if you find an inconsistency, what is the right answer? The function M can help us. Remember, when trying to construct M we do not have to specify the correct translation of all words. Instead, it is enough to look at say the most common 10.000 words. It is rather unlikely that we get the translations of these words wrong.
Next, compare the translations of rare words with the entry in the dictionary. How close are the word vectors? If there are far apart, a mistake might have occurred. In the case of finding different translations in different dictionaries, M can tell you which translation is more trustworthy. In the paper I have cited, “Exploiting Similarities among Languages for Machine Translation” by Mikolov et al., the authors experimented with this idea.
Admittedly, only in 15% of the cases, when M found a mistake (large distance), the dictionary entry was in fact inaccurate. However, this probably can be improved and is still useful as it stands. Imagine, looking instead for translation mistakes by just picking words randomly!
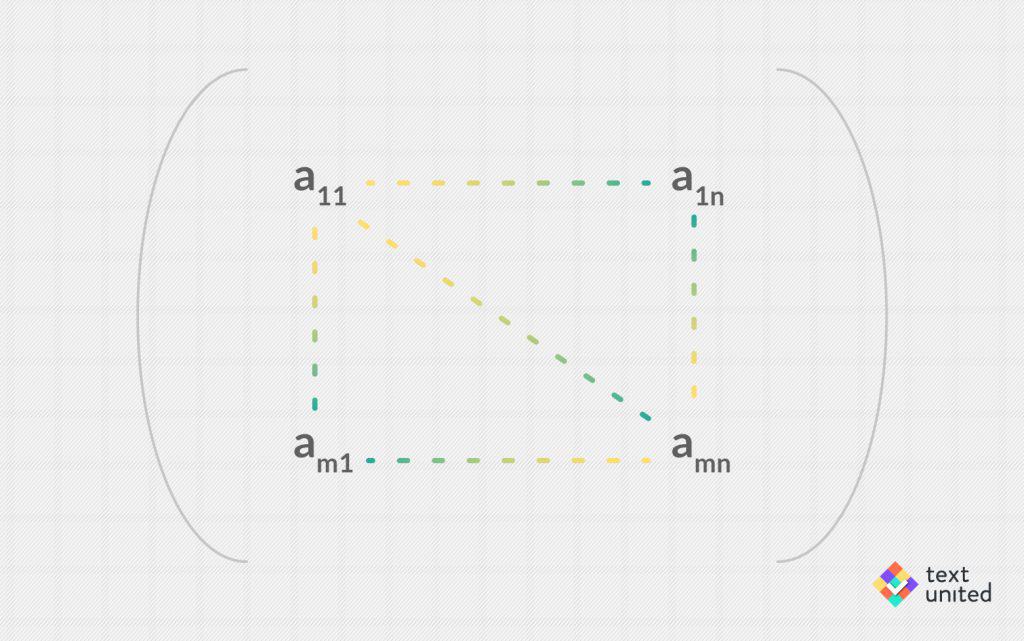
Last time I told you that the ‘M’ stands for ‘matrix’, which is a mathematical object. It consists of m rows and n columns (where m and n are natural numbers, say 12 and 15). The entries of the resulting grid are real numbers indexed by their respective position in the matrix.
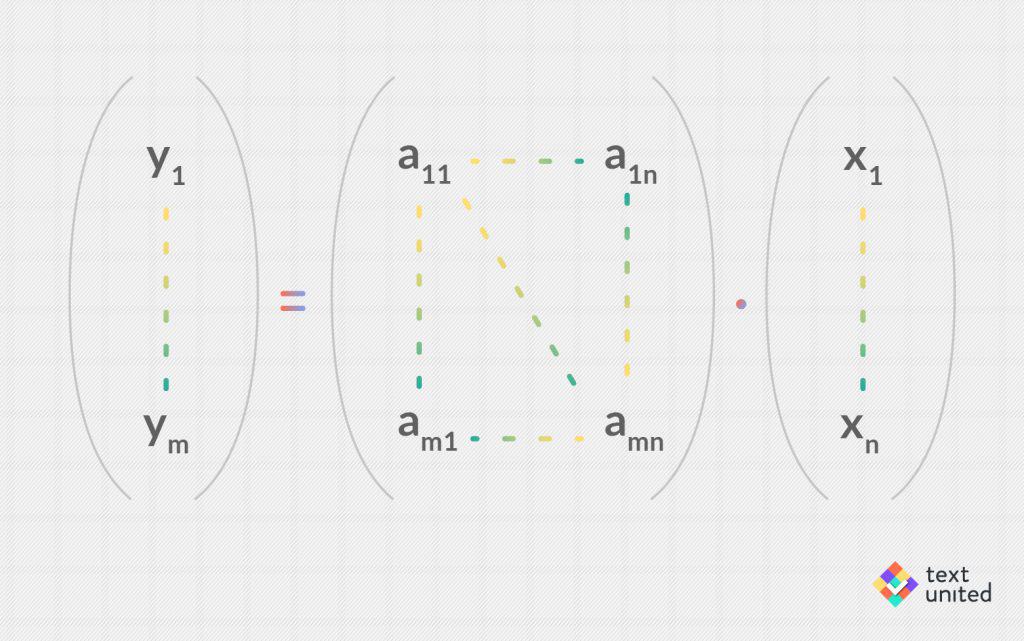
In total there are m times n entries, which completely specify the matrix. It turns out, that such matrices precisely correspond to linear mappings (like M) between an n-dimensional vector space and an m dimensional vector spaces. The mapping is usually written as a product:
In our case, n is the dimension of the source language vector space and m is the dimension of the target language vector space. That is why I have mentioned that in principle we just need to tell M what the correct translation is for about m times n words, and then it can generalize. In practice, it works, however, a bit different.
Just as learning the word vectors themselves, one can use a neural network to ‘learn’ how M should look like. I have spent already a few blog entries describing this process, so I will not repeat again here. Let me just mention that common words occur more often in the training data and so have a greater weight than rare words. Hence, the prerequisite for tackling bullet point number three is still fulfilled.
Next time we will take a closer look at more recent developments in the area of word vectors.
Stay Tuned!!