The first post in this series is here. The next post in this series is here.
If you are new here, in this series we are explaining what a Neural Network actually is and what it does, using an algorithm to recognize handwritten digits as an example. Later, we will dive into use neural networks in the natural language processing and eventually, in the neural machine translation. The purpose is to really show you what is going on behind the curtain, even if you are a completely new to this field!
In Part One we’ve focused on what a neuron is and in what way it makes connections. In the second part, we will go deeper and take a closer look at what a neural network does.
What Does The Neural Network Do?
First, we need to start with initializing all the neurons of the input layer, by plugging in some, possibly random, values. This will cause a chain reaction and the activation of the second layer, then the third and so on. The only thing that is now different compared to the case of just two neurons, is that each neuron has many inputs, hence is connected to many other neurons in the preceding layer.
In that case, we can sum up all the inputs to just one value and define this to be the actual input of a neuron. At the end of the chain, we end up with the activations in the output layer. As we have chosen the input randomly, we can expect to find just a bunch of meaningless numbers. The art of deep learning is to “teach” the neural network, to give us a specific output, when given a meaningful input. More generally machine learning refers to “teaching” in an analogous sense any program, not necessarily a neural network.
Next, let us consider a specific task. We would like to teach our neural network recognition of handwritten digits between 0 and 9:
The issue we face is how to use a digital picture of a handwritten number as input for our neural network. It turns out that the most naïve answer is actually the right one. Let’s assume the file fas a fixed size of 28×28 pixels. Let’s also assume it’s black and white. Like this, every pixel has just one number attached to it, its grayscale. Looking at this state of things, all information is contained in 28×28=784 numbers between 0 and 1 (with 0 corresponding to completely white and 1 to completely black).
Layer Construction
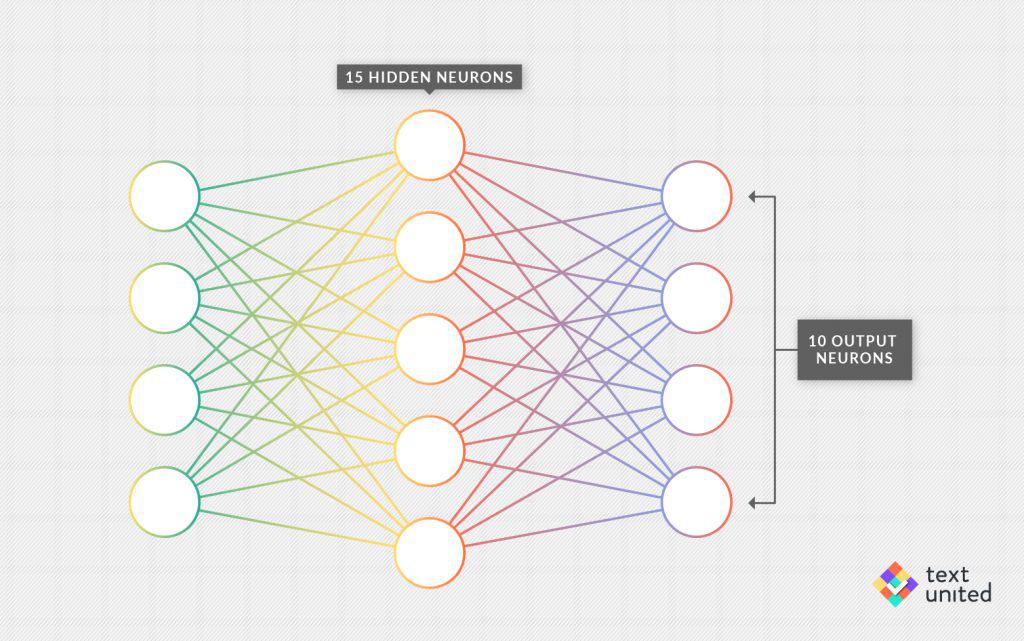
One might just go ahead and construct the first layer of a neural network with 784 input neurons, where we can later plug in all the grayscales of one digital picture. Now, what about the next layer? How many neurons will it contain? Well, there does not seem to be a unique right answer. We have to decide it simply by trial and error.
The number of neurons in the so-called hidden layers, layers other than the input and output layer, is a hyperparameter. Hyperparameters are parameters that are not learned by the machine but have to be chosen beforehand by the programmer. Another hyperparameter example would be the depth of a neural network, which corresponds to the number of hidden layers.
Michael Nielsen, a world-known scientist, writer and programmer works with three layers on his blog. If you think about it, one layer is hidden, consisting of 15 neurons. And what about the output layer? That’s the easiest part; it will just contain ten neurons corresponding to the ten digits from 0 to 9.
Now what we want to happen is roughly the following. We give as input the 784 grayscales comprising on a digital picture of some handwritten digit. What happens next? The neurons in the hidden layer get activated, which results in an activation of the output neurons. The hope is that just one neuron will light up, namely the one from the input picture. That’s a lot to hope for. We would need to find the right weights (there are 784×15+15×10 ≈ 12000 of them) for this to work.
At the moment it is not at all clear that this is possible in principle, let alone whether we can implement it. In the next blog, we will explain how this is done. The key will be machine learning, which mathematically is just optimization by gradient descent. An idea that goes back to Isaac Newton. See you next month!